3260. Сколько?

Готовясь к экзамену по математическому анализу, Петя разложил перед собой n разных шпаргалок. Они были его спасением, ведь за весь семестр Петя так ни разу не удосужился учить материал как следует. Шпаргалок оказалось настолько много, что они не вмещались ни в один карман. Поэтому Петя решил подсчитать максимальное количество шпаргалок, которое он сможет взять с собой на экзамен. И тут возник вопрос: а сколько вообще существует способов выбрать нужное количество шпаргалок?

Вход. Содержит общее количество шпаргалок n (1 ≤ n ≤ 12) и количество шпаргалок k (0 ≤ k ≤ n), которое Петя может взять с собой.

Выход. Выведите количество способов выбрать k шпаргалок из n.

Пример входа 1	Пример выхода 1
3 2	3
Пример входа 2	Пример выхода 2
4 1	4

РЕШЕНИЕ

комбинаторика

Анализ алгоритма

Для вычисления биномиального коэффициента можно воспользоваться следующим соотношением:

==

Объявим переменную res и инициализируем ее значением 1. Затем умножим res на n и разделим результат на 1. После этого умножим res на n – 1 и разделим на 2. Процесс умножений и делений будем продолжать k раз (числитель и знаменатель после сокращения на (n – k)! содержит k множителей).

Для рекурсивной реализации биномиального коэффициента можно воспользоваться соотношением:

=

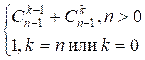
Реализация алгоритма

Функция Cnk вычисляет значение биномиального коэффициента итеративным методом.

int Cnk(int n, int k)

{

int res = 1;

for(int i = 1; i <= k; i++)

res = res * (n - i + 1) / i;

return res;

}

Основная часть программы. Читаем входные данные.

scanf("%d %d",&n,&k);

Вычисляем и выводим ответ.

res = Cnk(n,k);

printf("%d\n",res);

Реализация алгоритма – рекурсия

Функция Cnk вычисляет значение биномиального коэффициента рекурсивным методом.

int Cnk(int n, int k)

{

if (n == k) return 1;

if (k == 0) return 1;

return Cnk(n - 1, k - 1) + Cnk(n - 1, k);

}

Основная часть программы. Читаем входные данные.

scanf("%d %d",&n,&k);

Вычисляем и выводим ответ.

res = Cnk(n,k);

printf("%d\n",res);

Реализация алгоритма – рекурсия с запоминанием

Объявим массив dp для запоминания значений биномиального коэффициента: dp[n][k] = .

int dp[35][35];

Функция Cnk вычисляет значение биномиального коэффициента рекурсивным методом. Используем технику мемоизации.

int Cnk(int n, int k)

{

if (n == k) return 1;

if (k == 0) return 1;

if (dp[n][k] != -1) return dp[n][k];

return dp[n][k] = Cnk(n - 1, k - 1) + Cnk(n - 1, k);

}

Основная часть программы. Читаем входные данные.

scanf("%d %d",&n,&k);

Инициализируем массив dp.

memset(dp,-1,sizeof(dp));

Вычисляем и выводим ответ.

res = Cnk(n,k);

printf("%d\n",res);

Java реализация – рекурсия

import java.util.*;

public class Main

{

static int Cnk(int n, int k)

{

if (n == k) return 1;

if (k == 0) return 1;

return Cnk(n - 1, k - 1) + Cnk(n - 1, k);

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int k = con.nextInt();

int res = Cnk(n,k);

System.out.println(res);

con.close();

}

}

Java реализация – рекурсия с запоминанием

import java.util.*;

public class Main

{

static int dp[][];

static int Cnk(int n, int k)

{

if (n == k) return 1;

if (k == 0) return 1;

if (dp[n][k] != -1) return dp[n][k];

return dp[n][k] = Cnk(n - 1, k - 1) + Cnk(n - 1, k);

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int k = con.nextInt();

dp = new int[n+1][k+1];

for(int i = 0; i <= n; i++)

Arrays.fill(dp[i],-1);

int res = Cnk(n,k);

System.out.println(res);

con.close();

}

}

Python реализация – comb

Для вычисления биномиального коэффициента воспользуемся встроенной функцией comb(n, k) = .

import math;

Читаем входные данные.

n, k = map(int, input().split())

Вычисляем и выводим ответ.

res = math.comb(n, k)

print(res)

Python реализация – факториал

Функция fact(x) вычисляет факториал числа x.

def fact(x):

if x:

return fact(x - 1) * x

else:

return 1

Основная часть программы. Читаем входные данные.

n, k = map(int, input().split())

Вычисляем и выводим ответ.

res = fact(n) // (fact(k) * fact(n - k))

print(res)

Python реализация – рекурсия с запоминанием

Функция Cnk вычисляет значение биномиального коэффициента рекурсивным методом. Используем технику мемоизации.

def Cnk(n, k, dp):

if n == k: return 1

if k == 0: return 1

if dp[n][k] != -1: return dp[n][k]

dp[n][k] = Cnk(n - 1, k - 1, dp) + Cnk(n - 1, k, dp)

return dp[n][k]

Основная часть программы. Читаем входные данные.

n, k = map(int, input().split())

Объявим список dp для запоминания значений биномиального коэффициента: dp[n][k] = .

dp = [[-1] * 35 for _ in range(35)]

Вычисляем и выводим ответ.

res = Cnk(n, k, dp)

print(res)